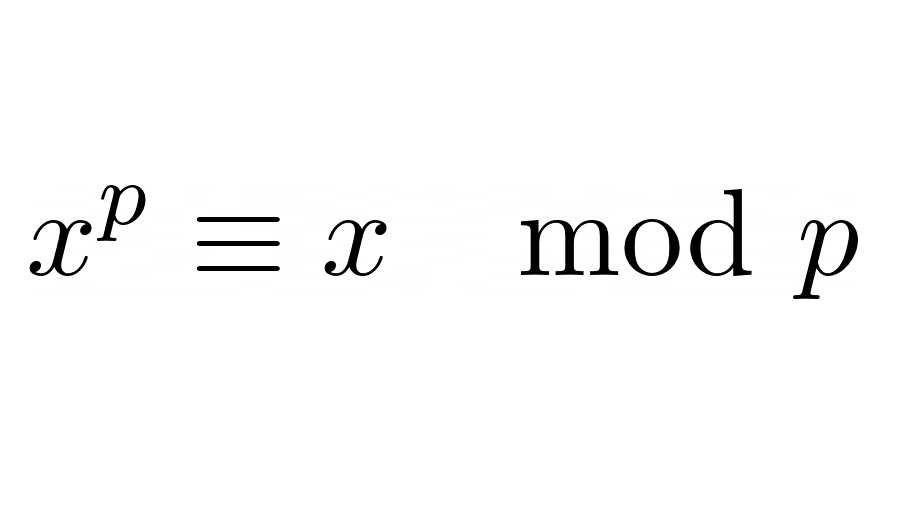Matematikos šaka, tirianti veiksmų su įvairiais dydžiais (reiškiamais raidėmis) bendrąsias savybes, nepriklausomas nuo tų dydžių kilmės. Algebra yra viena seniausių matematikos šakų, atsiradusi senovės Rytų civilizacijose, kur buvo ieškoma apibendrintų metodų panašiems uždaviniams spręsti.
Algebroje sprendžiami dydžių sistemose kylantys uždaviniai, kai dydžių sistemos klasifikuojamos pagal veiksmų savybes. Skirtingai nei matematinėje analizėje ar funkcijų teorijoje, algebroje nėra ribos sąvokos.